(1) バイナリサーチ（二分探索法）

バイナリサーチ（二分探索法）とは

バイナリサーチ（二分探索法）は、要素が昇順(または降順)に並んでいる配列に対して高速に探索できるアルゴリズムです。調べる範囲を半分に絞りながら探す方法なので、２つ（バイナリ）に分けて探索ことから、バイナリサーチといいます。

手順

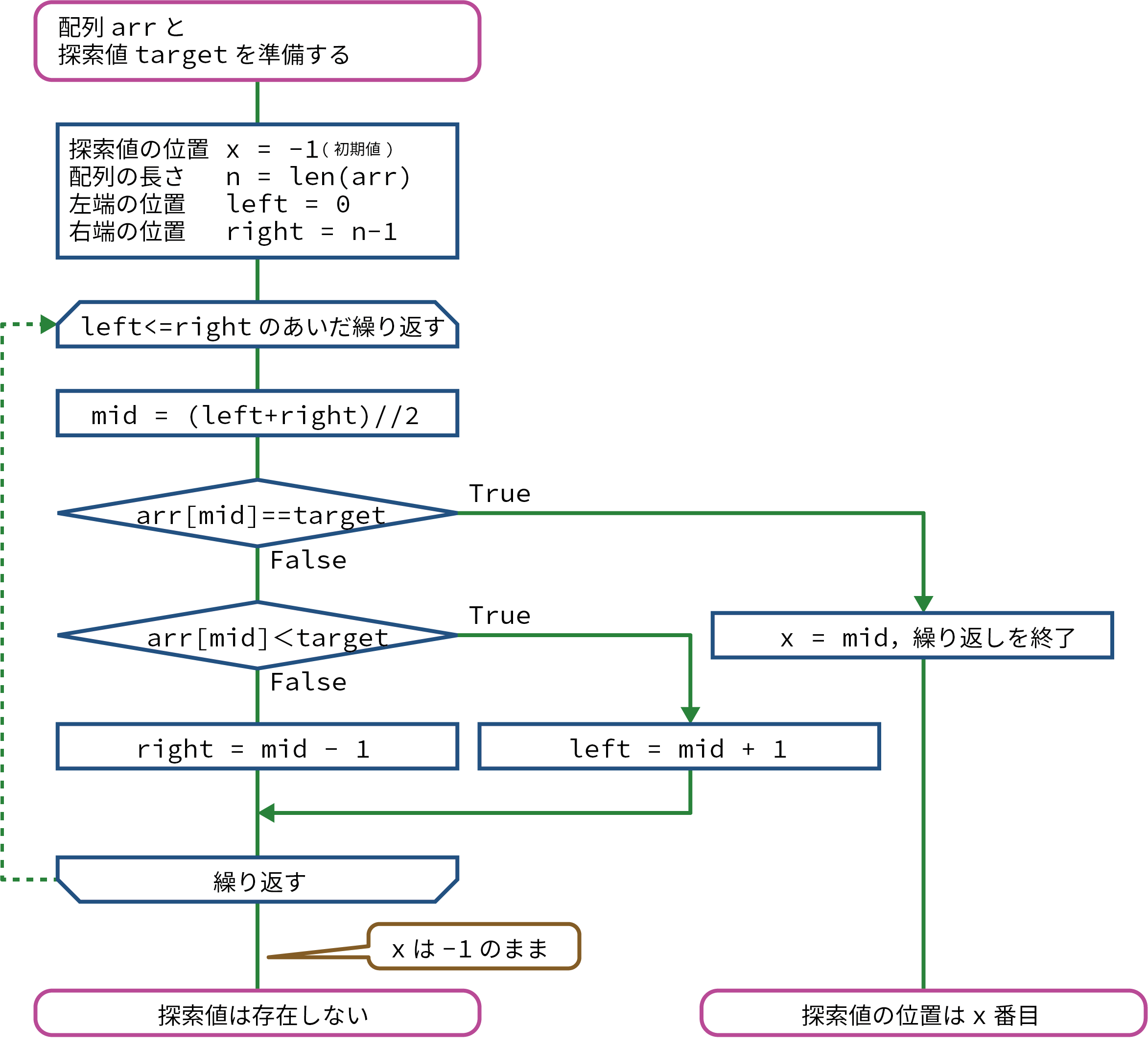
昇順（または降順）に並んでいる配列に対して、次の操作をします。

1. 探索範囲(最初は全範囲)の左端の位置(left)と右端の位置(right)を決めます。
2. 探索範囲の中央の位置(mid)を求めます: mid = (left + right) // 2。
3. 中央値(arr[mid])が探索値(x)と一致したら、中央の位置(mid)が探索値の位置となり、探索を終了します。
4. 中央値が探索値より小さければ(arr[mid] < x)、中央の位置よりも左側にはより小さい値しかないので、左半分を調べる必要はなくなります。
   よって、探索範囲を右半分にすればよいので、探索範囲の左端を中央の位置より１つ右にします(left = mid + 1)。
5. 中央値が探索値よりも大きければ(arr[mid] > x)、中央の位置よりも右側にはより大きい値しかないので、右半分を調べる必要はなくなります。
   よって、探索範囲を左半分にすればよいので、探索範囲の右端を中央の位置より１つ左にします(right = mid - 1)。
6. 探索範囲にデータが存在する間は、(2)〜(5)を繰り返します。

フローチャート

デモンストレーション

プログラム（基本）

上記の手順をプログラムに書くと、次のようになります。

Colaboratoryのノートブックに書き写しながら、理解しましょう。

        arr = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19]
        print(arr)
        target = int(input("探索値:"))

        x = -1          # 探索値のインデックス番号（初期値: -1）
        n = len(arr)

        left = 0        # 探索範囲の左端の位置
        right = n - 1   # 探索範囲の右端の位置

        while left <= right:                # 探索範囲の左端と右端の間にデータがある限り繰り返す
          mid = (left + right) // 2       # 探索範囲の中央の位置
          if arr[mid] == target:          # 中央値＝探索値のとき
            x = mid                     # xに中央の位置を代入して終了
            break
          elif arr[mid] < target:         # 中央値＜探索値のとき、左端を中央の位置より１つ右に移動する
            left = mid + 1
          else:                           # 中央値＞探索値のとき、右端を中央の位置より１つ左に移動する
            right = mid - 1

        if x != -1:
          print(target, "のインデックス番号は", x)
        else:
          print(target, "は存在しません。")
      

        [1, 3, 5, 7, 9, 11, 13, 15, 17, 19]
        探索する数値:5    #5を入力した場合
        5 のインデックス番号は 2
      

探索回数

\(n = 8\)の配列[0, 1, 2, 3, 4, 5, 6, 7]をバイナリサーチしたときに、各数字が見つかるときの探索回数は次の表の通りです。

また、\(n = 15\)の配列[0, 1, 2, ･･･, 14]をバイナリサーチしたときに、各数字が見つかるときの探索回数は次の表の通りです。

また、\(n = 16\)の配列[0, 1, 2, ･･･, 15]では次の通りです。

最小探索回数

最小探索回数は、探索値が中央にあった場合なので１回です。

最大探索回数

最大探索回数は、上記の具体例からもわかるとおり、データ数を \(n\) 個とすると、\(2^x \leqq n < 2^{x+1}\) のとき、最大探索回数は \(x+1\) 回と表せます。

これを対数を用いて表すと \(x \leqq \log_2 n < x+1\) となり、\(\log_2 n\) の整数部分が \(x\) となることから、ガウス記号を用いて \(x=[\log_2 n]\) と表すことができます。したがって、最大探索回数は \([\log_2 n]+1\) 回となります。

※\(2^3 = 8 \) は、対数を用いると \(\log_2 8 = 3\) と表せます。

平均探索回数

バイナリサーチの平均探索回数を厳密に求めることは大変なので、次のように考えます。

最大探索回数の1回前までで全データの半分以上を探索することができるので、平均探索回数は\([\log_2 n]\) 回となります。

最大探索回数の比較

リニアサーチとバイナリサーチの探索回数を比較すると、次のようになります。

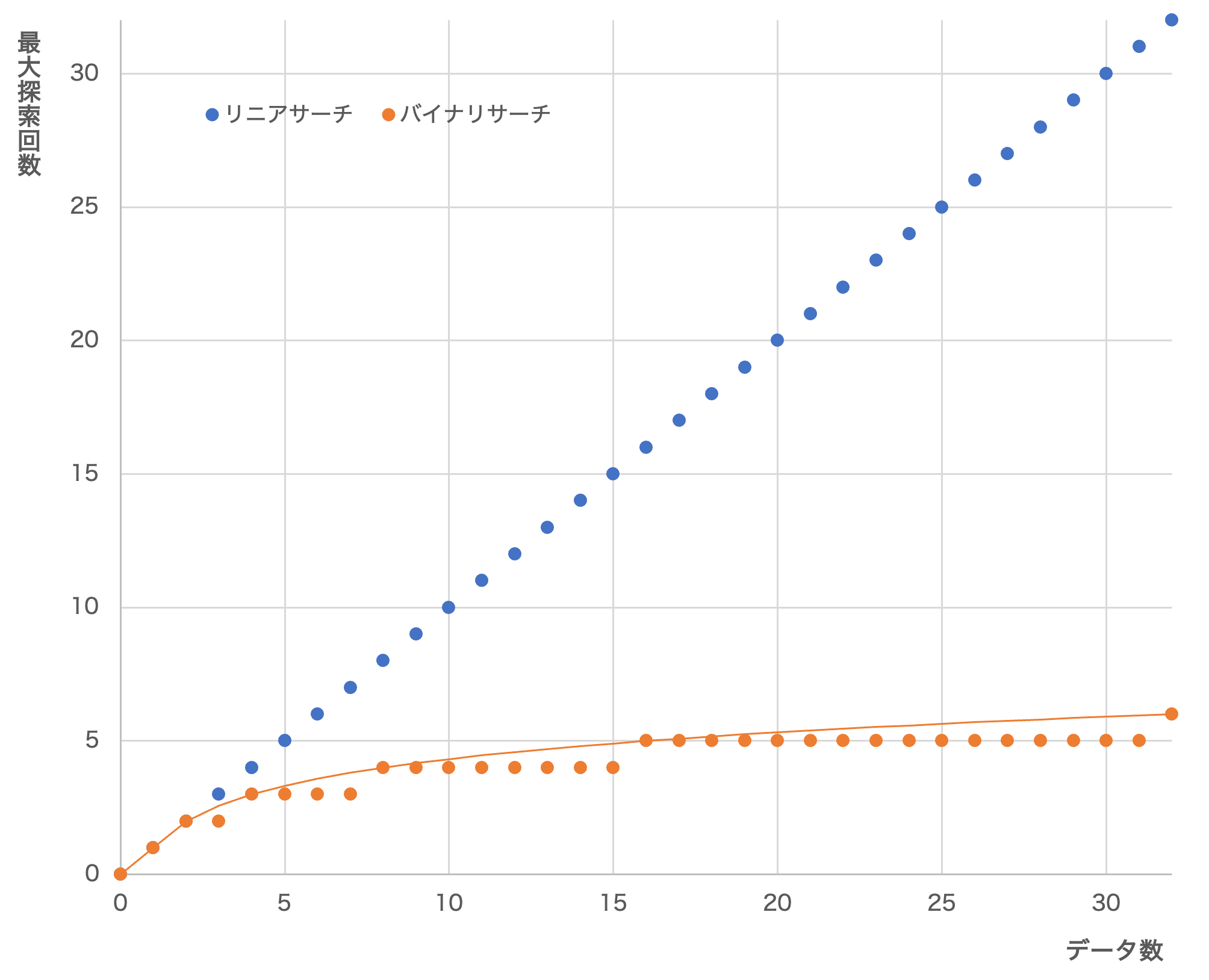
データ数が多くなっても、バイナリサーチはリニアサーチに比べてあまり増加しないことがわかります。バイナリサーチでは、データ数が２倍になっても、探索回数は１回増えるだけなので、効率がいい探索方法であることがわかります（ただし、データが昇順または降順に並んでいる必要があります）。

練習問題

リニアサーチ（線形探索）とバイナリサーチ（二分探索）の探索効率の違いについて、次の各問いに答えなさい。ただし、はじめは自分の力のみで考えて（紙とペンのみ使用可）、その後実際にコードを作成して確かめなさい。

連番の配列[0, 1, 2, ..., 15]を生成するには、次のように書きます。

arr = list(range(16))

問1

0以上の整数が昇順に並んだ \(n\) ＝16の配列[0, 1, 2, 3, ・・・, 15]について、次の探索値が見つかるまでの回数（探索回数）はいくつか。

問2

0以上の整数が昇順に並んだ \(n\) ＝256の配列[0, 1, 2, 3, ・・・, 255]について、次の探索値が見つかるまでの回数（探索回数）はいくつか。