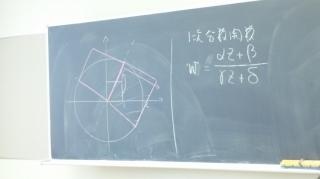昨日までは、いわば「準備編」であったリレー講座。後半の三日間はいわゆる「複素関数論」の初歩を垣間見ます。
後半戦の初日は平山先生による「複素数平面上の幾何」と「複素数の関数」の解説です。まずは昨日の内容を復習された(写真1)あと、平面図形を複素数平面に配置して、複素数を利用した直交条件などを概観(写真2)。「複素数平面の上に置く？そんなことをしても大丈夫なのかなぁ…」といった感じの中1生が少なくなく、また受講者全体から「さすがにこれは前半戦よりは手強いぞ」という雰囲気がひしひしと感じられます。ちなみに、このリレー講座は他校からも先生が来訪されて、聴講されております(写真3)。
そして、いよいよ本講座の本題といえる複素関数の話題に突入しました(写真4)。
まずは一次関数を具体的に与え「幾何学的に」考察。果たして一次関数とは回転と平行移動の合成となることが示され(写真5)、大いに頷く中３生（数学部員の由）が印象的でした。
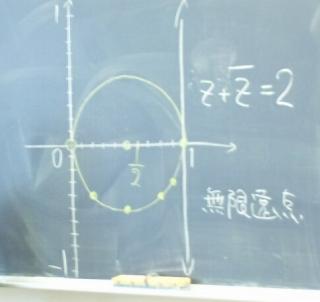
最後は一次分数関数にまで話題はおよび、具体例を用いて、いわゆる「円円対応」を解説されました。これは、複素数平面上の「円または直線」は一次分数関数によって「円または直線」に写ることを述べたものです。（写真6）に見ることのできる“無限遠点”の導入により，複素平面上の円は「リーマン球面」上の円と捉えることができることからこのように呼ばれているようです。
さすがに、時間の制約からリーマン球面についての詳しい言及はなされなかったのですが、このリーマン球面が明日のテーマの理解をするための鍵を握っています。
それにつけても、さすがに数学愛好者の集う本講座。欠席者が殆どいません。この調子でラストまで駆け抜けてください。(数学科)

（写真１）

（写真２）

（写真３）

（写真４）

（写真５）

（写真６）

　最終日は，化石採集がメインでした。この日は葛生地域を訪れ，葛生化石館の奥村学芸員の案内で，化石館の見学と化石採集を行いました。午前中に，化石館で展示の見学と解説，この地域の化石の特徴を勉強し，昼前から採集に出掛けました。現地では，少し山を登り，古生代のペルム紀の石灰岩をたたくと，フズリナ，ウミユリ，腕足類，コケムシ，サンゴなどの化石が採集できました。炎天下でしたが，山の中は木陰で心地よい風が吹き，化石も採れたので，とても良い一日になりました。
　3日間，多くの方々にお世話になりました。どの方も熱心に面倒を見ていただき，とても幸せな巡検旅行だったと思います。ありがとうございました。感謝の気持ちを忘れずに。

葛生化石館の見学